This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Sam Bowyer, Equal contribution, Department of Mathematics and sam.bowyer@bristol.ac.uk;
(2) Thomas Heap, Equal contribution, Department of Computer Science University of Bristol and thomas.heap@bristol.ac.uk;
(3) Laurence Aitchison, Department of Computer Science University of Bristol and laurence.aitchison@bristol.ac.uk.
Table of Links
- Abstract & Introduction
- Related work
- Background
- Methods
- Experiments
- "Conclusion, Limitations, and References"
- Derivations
- Algorithms
- Experimental Datasets And Model
Experiment
We provide empirical results comparing the global and massively parallel importance weighting/sampling methods, as well as VI and HMC baselines. We considered two datasets: MovieLens100K (Fig. 1) and NYC Bus Breakdown (Fig. 2). MovieLens100K (Harper and Konstan 2015) contains 100k ratings of N=1682 films from among M=943 users. NYC Bus Breakdown describes the length of around 150,000 delays to New York school bus journeys, segregated by year, borough, bus company and journey type. We use hierarchical probabilistic graphical models for these datasets, which are described in more detail in Appendix section Experimental Datasets And Models.
For global and massively parallel importance sampling, we use the prior as a proposal. For VI, we used a factorised approximate posterior and optimized using Adam with learning rates ranging from 10−2 to 10−4 (learning rates faster than 10−2 were unstable). For HMC, we used the NUTS (Hoffman, Gelman et al. 2014) implementation from PyMC (Salvatier, Wiecki, and Fonnesbeck 2016).
We consider four quantities in Fig. 1 and Fig. 2. We begin by looking at the ELBO (Fig. 1a,2a). While massively parallel estimates of the ELBO can be computed using previous methods (e.g. Heap and Laurence 2023), it is nonetheless useful as it is a good measure of the quality of our approximate posteriors (as the ELBO can be written as the sum of the marginal likelihood and the KL-divergence between the true and approximate posterior Jordan et al. 1999; Kingma, Welling et al. 2019). Next, we plot the predictive log-likelihood, based on posterior samples obtained using
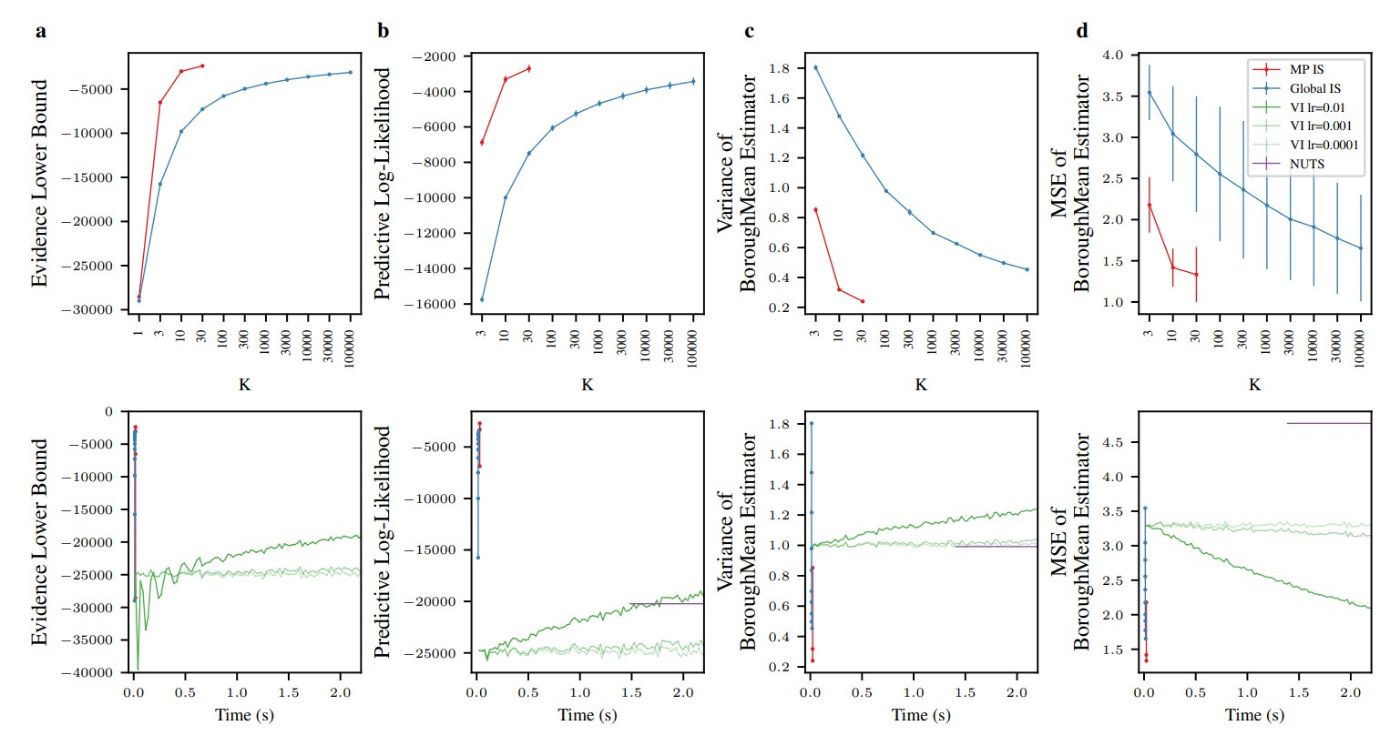
the approach in the Methods section. In both of these plots, we see dramatic improvements against standard “global” importance sampling for a fixed K (top row), and for a fixed time against other baselines such as VI and HMC (bottom row). Finally, we consider the quality of the posterior moment estimates computed using the approach in the Methods section. In particular we consider two measures of the quality of our posterior mean estimator. First, we consider the variance of the estimator (Fig. 1c,2c); in the ideal case, when we have exactly computed the posterior mean, this variance should be zero. While this variance can be zero in other cases (e.g. when the mean estimator always returns a constant), it does provide a lower-bound on the expected squared error between the estimator and the true value. Second, we directly considered the MSE between our posterior mean estimator and the true latent variable (Fig. 1d,2d). However, this quantity requires us to know the true value for the latent variable, which requires us to generate data from the model (we only generated data for d, columns a–c use real data). Again, in both of these cases, we see dramatic improvements for massively parallel against standard “global” importance sampling for a fixed K (top row), and for a fixed time against other methods such as VI and HMC (bottom row).
Note the extremely poor performance of VI and HMC is because these are iterative methods that take many steps, and hence a long time to reach good performance. HMC is especially problematic on these short timescales, because it needs many gradient steps before it returns even a single posterior sample (and this is ignoring burn-in and adaptation phases). In contrast, importance sampling gets a reasonable answer much more quickly, as it just a single, non-iterative computation.
