Authors:
(1) Renan F. F. da Silva, Institute of Computing, University of Campinas;
(2) Yulle G. F. Borges, Institute of Computing, University of Campinas;
(3) Rafael C. S. Schouery, Institute of Computing, University of Campinas.
6 Variable Neighborhood Search

6.1 Objective function
Our objective function f has two levels: the primary objective that seeks to minimize the number of used bins and the secondary objective that seeks the lowest lexicographic order in the residual vector. The residual vector consists of the residual capacity of used bins in non-decreasing order.

6.2 Neighborhoods
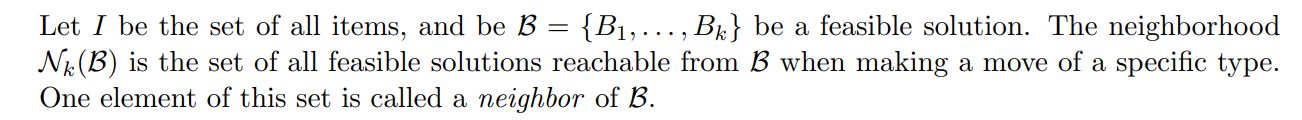
The VNS performs local searches in neighborhoods, as will be explained below. One relevant factor is the heuristic used in the local search. In our VNS, we use the Best Improvement heuristic, which analyzes all neighbors of a solution and changes to the best neighbor (in terms of the objective function).
Our VNS has neighborhoods with the moves: Move-Item, Swap-Items, Swap-and-Move, and MoveTwo-to-One. The number of items changed in one move is constant for these neighborhoods, which just change a constant number of bins and elements in the residual vector (of the second objective function). As we can compare two neighborhoods using their variations in the objective function, it can be done in O(1). Next, we present our neighborhoods, showing optimizations to obtain fast algorithms even for large instances.
6.2.1 Move-Item Neighborhood
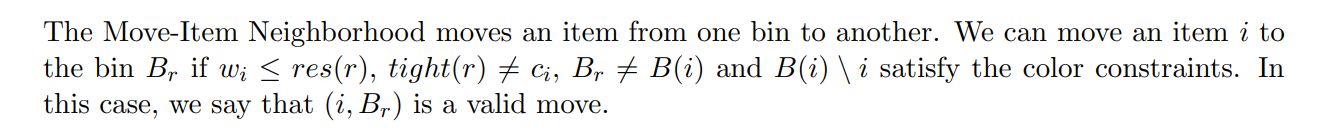
For the CBPP, one possible algorithm for this neighborhood is to adapt the algorithm used by Fleszar and Hindi [19] for the BPP, that have time complexity O(n2). In this, for each item i, we iterate in the bins given in non-ascending order of residual capacity. Then, we check if the move (i, Br) is valid, where Br is the current bin, and evaluate it if so. Besides, we stop the search when we find the first bin Br such that wi > res(r), since the ordering guarantee that the bins forward also do not have space for the item i.
However, it is not necessary to evaluate all moves to find the best one. Applying the Auxiliary Algorithm using the current solution B, it returns the best move for each item i ∈ I, so the best one is the best move between them. It gives us an implementation of the Move-Item Neighborhood with time complexity Θ(n).
6.2.2 Swap-Items Neighborhood

Fleszar and Hindi [19] propose for the BPP a Swap-Items Neighborhood with complexity O(n+M), where M is the number of valid moves, which can be very fast in some solutions with little free space. We present the pseudocode of this neighborhood in the Algorithm 4.

Although the time complexity of this algorithm is O(n log n + M), in our tests, it performed better than Fleszar and Hindi’s algorithm, especially in large instances. Algorithm 5 presents the pseudocode of this algorithm.

6.2.3 Move-Two-to-One Neighborhood

6.2.4 Swap-and-Move Neighborhood
The Swap-and-Move Neighborhood selects three items i, j, k from different bins, then swaps i and j, and moves k to B(i) (its bin before the move). This neighborhood has complexity O(n3) when implemented in the completed way, which offers a low cost-benefit, so we use a restricted version from this one.
Instead of testing all the possibilities of k, we test only the heaviest item that can be moved to B(i). The first candidate for k is the heaviest item that fits in B(i), and we can use a binary search to find it.


6.3 Shake Algorithm
The Shake Algorithm is a function that makes random moves, seeking to escape from local optimal. In particular, our Shake chooses to execute one of two subroutines with equal probability. In the first subroutine, we performed 20 moves with the constraint that each bin belongs to a maximum of one move. The possible moves are to move one item or swap two items. In the second subroutine, we select two bins and then repack their items in a random order using the Best Fit heuristic.
Note that we use a very aggressive Shake since its moves can make the solution much worse. Our Shake is based on the one proposed by Fleszar and Hindi [19] for the BPP, which is equal to the first subroutine without the constraint that bins must be distinct in different moves. The second routine was added because the perturbation generated by the first one can be small in instances with little free space.
6.4 Algorithm

6.5 Neighborhood Ordering
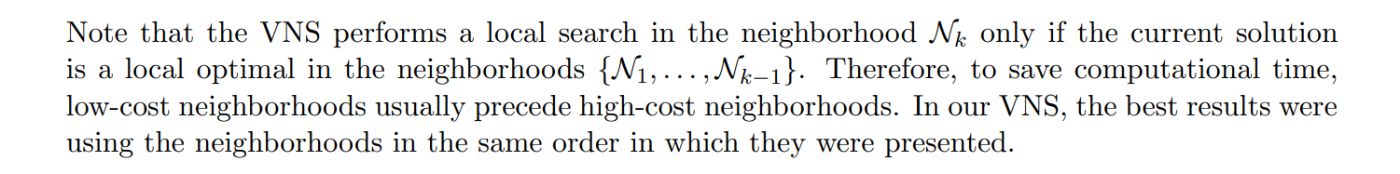
This paper is available on arxiv under CC 4.0 license.
