Fundamentals of Graph Theory
A graph is a mathematical structure used to model pairwise relationships between objects. A graph consists of a set of vertices (or nodes) and a set of edges, each of which connects a pair of vertices. This allows the representation of various data as networks, including road networks, social connections, relationships between different business processes, and more.
Graphs can be directed or undirected. In a directed graph, edges have a direction indicating from one vertex to another, whereas in an undirected graph, edges have no directionality.
0 ------ 1
/ \ | \
/ \ | \
2 --- 3 | 4
\ / \ | /
\ / \ | /
5 ------ 6
What is a tree in the context of graph theory?
In the context of graph theory, a tree is a special case of a graph. It is an undirected graph that is connected and acyclic. Trees exhibit several interesting properties, such as there being exactly one path between any two vertices. This makes them ideal for use in data structures such as search trees, parsing trees, process management structures, and more.
1
/ \
2 3
/ \ \
4 5 6
/
7
In problem-solving, we may also encounter binary trees.
A binary tree is a hierarchical data structure in the form of a tree, consisting of nodes (vertices), where each node has at most two children: a left child and a right child. Each node contains some data (value) and references (pointers) to its child nodes.
Key characteristics of a binary tree:
- Root: This is the topmost node of the tree, from which the entire structure originates. A binary tree has exactly one root.
- Children:
- Each node can have a maximum of two children: a left child and a right child.
- Left Child: The node positioned to the left of the current node.
- Right Child: The node positioned to the right of the current node.
- Leaves:
- These are nodes in the binary tree that do not have any children (i.e., their
leftandrightpointers arenull).
- These are nodes in the binary tree that do not have any children (i.e., their
- Height of the Tree:
- The height of a tree is defined as the maximum number of levels from the root to the furthest leaf node. An empty tree (with no nodes) has a height of 0, and a tree with only one node (just the root) has a height of 1.
- Level of a Node:
- The level of a node is determined by the number of edges on the path from the root to that node. The root node is at level 0.
A binary tree is a fundamental data structure used in computer science and programming for a variety of applications, including binary search trees, expression trees, binary heaps, and more. Understanding the properties and operations of binary trees is essential for implementing efficient algorithms and solving various computational problems.
It's time to look at some examples.
Graph
To begin with, I'd like to suggest implementing a basic graph construction first, and then we'll see how we can use it in problems. We'll create a simple representation of a graph using adjacency lists.
import java.util.*;
class Graph {
private int V; // Number of vertices
private LinkedList<Integer>[] adj; // Adjacency list representation
Graph(int v) {
V = v;
adj = new LinkedList[v];
for (int i = 0; i < v; ++i) {
adj[i] = new LinkedList();
}
}
void addEdge(int v, int w) {
adj[v].add(w); // Add w to v's adjacency list
adj[w].add(v); // Add v to w's adjacency list (for undirected graph)
}
public static void main(String[] args) {
Graph graph = new Graph(5);
graph.addEdge(0, 1);
graph.addEdge(0, 4);
graph.addEdge(1, 2);
}
}
To work with graphs, we use just two important algorithms: DFS and BFS. Let's look at them and go through the theory.
Depth-First Search (DFS)
DFS (Depth-First Search) is an algorithm for traversing or searching in a graph or tree. It starts by choosing an initial vertex and then moves to its adjacent vertices. Once a vertex is reached that has no unvisited neighbours, the algorithm backtracks and continues exploring other branches. The main idea of DFS is to go as deep as possible into the data structure before backtracking.
Key steps of DFS:
-
Visit the current vertex.
-
Recursively call DFS for each adjacent unvisited vertex.
DFS can be used for various tasks such as finding paths between vertices, determining graph connectivity, topological sorting, and others.
Let’s check the problem: https://leetcode.com/problems/keys-and-rooms/. We realized that we can solve this using a graph and DFS, but how? Instead of simple rooms, we have a graph here. We can start at position 0 without any keys, but we can move further. In our problem, we need to track the rooms we have visited. Therefore, we create a boolean array and mark room zero as visited.
boolean[] seen = new boolean[rooms.size()];
seen[0] = true;
In Java, we can use the Stack class to help maintain the order of our elements (Last-In-First-Out, or LIFO). We can push our nodes onto the stack.
while (!stack.isEmpty()) {
int curruentNode = stack.pop();
for (int n: rooms.get(curruentNode))
if (!seen[n]) {
seen[n] = true;
stack.push(n);
}
}
}
The final step is to check if there are any unvisited rooms left. If we find an unvisited room, we return false, indicating that not all nodes have been visited. Otherwise, we return true, indicating that we have visited all nodes.
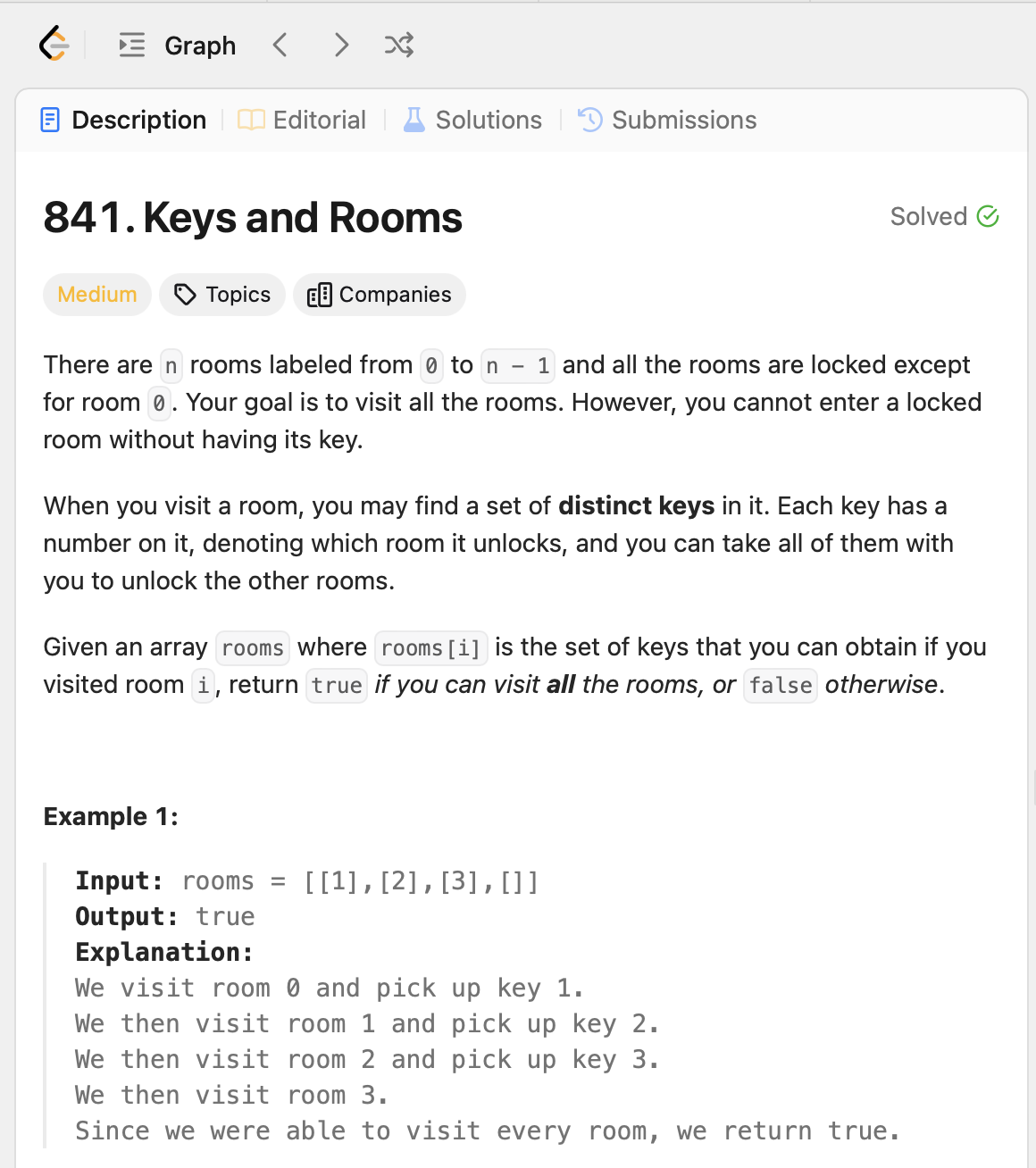
class Solution {
public boolean canVisitAllRooms(List<List<Integer>> rooms) {
boolean[] seen = new boolean[rooms.size()];
seen[0] = true;
Stack<Integer> stack = new Stack();
stack.push(0);
while (!stack.isEmpty()) {
int curruentNode = stack.pop();
for (int n: rooms.get(curruentNode))
if (!seen[n]) {
seen[n] = true;
stack.push(n);
}
}
for (boolean v: seen) {
if (!v) {
return false;
}
}
return true;
}
}
Breadth-First Search (BFS)
BFS (Breadth-First Search) is an algorithm for traversing or searching in a graph or tree. It starts by choosing an initial vertex and explores all of its neighbours at the current level before moving to neighbours of neighbours in the next level. In other words, it processes all adjacent vertices of the current vertex before moving on to adjacent vertices of those vertices and so on.
Key steps of BFS:
- Enqueue the initial vertex into a queue.
- While the queue is not empty, dequeue a vertex from the front of the queue.
- Visit the current vertex and enqueue all its unvisited adjacent vertices to the back of the queue.
- Repeat steps 2-3 until the queue is empty.
BFS is often used for finding the shortest path in unweighted graphs, checking graph connectivity, level-order traversal in trees, and other applications where it's necessary to process all vertices of a specific level before moving to the next level.
Let’s check this one: https://leetcode.com/problems/same-tree/ As we can see, we already have a class TreeNode (we are near the topic, yes).
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
And what do we need to do? We should use recursion and check all nodes. Let’s start with checking nodes:
boolean left = isSameTree(p.left, q.left);
boolean right = isSameTree(p.right, q.right);
boolean result = left && right;
But we need to stop the recursion call and for the case, we should add base cases:
- all nodes are null
if (p == null && q == null) return true;
- One node isn’t null
if (p == null || q == null) return false;
- Values aren’t equels
if (p.val != q.val) return false;
And finally, we’ll add the return statement:

/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public boolean isSameTree(TreeNode p, TreeNode q) {
if (p == null && q == null) return true;
if (p == null || q == null) return false;
if (p.val != q.val) return false;
boolean left = isSameTree(p.left, q.left);
boolean right = isSameTree(p.right, q.right);
return left && right;
}
}
Conclusion
Graphs and Trees:
Graphs and trees are important data structures in computer science used for modelling and analyzing complex relationships between objects. They find wide applications in various fields including algorithms, network modelling, databases, bioinformatics, and more.
Key Characteristics of Graphs and Trees:
- Graphs can be directed or undirected, contain cycles or be acyclic.
- Trees are a special case of graphs that are connected and acyclic.
- In graphs, each element is called a vertex, and the connections between vertices are called edges.
DFS (Depth-First Search):
-
Allows traversal of a graph or tree in a depth-first manner.
-
Uses a stack for the recursive traversal of vertices.
-
Applied for pathfinding, connectivity checking, topological sorting, and other tasks.
BFS (Breadth-First Search):
- Allows traversal of a graph or tree in a breadth-first manner.
- Uses a queue for systematic exploration of neighbours at each level.
- Applied for shortest path finding, connectivity checking, level-order traversal, and other tasks.

