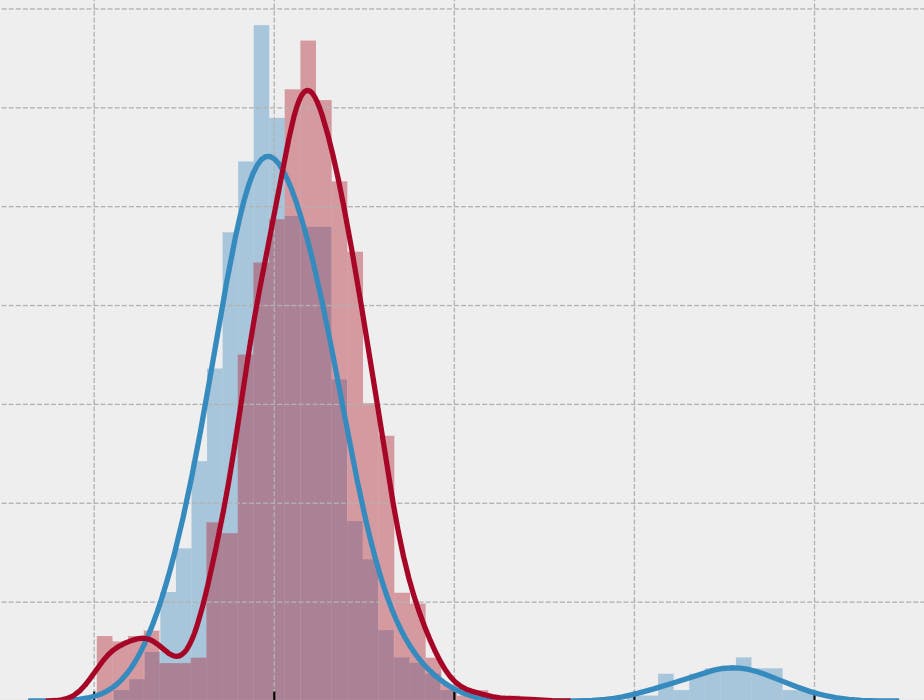
Analysts often encounter outliers in data during their work, such as during AB-test analysis, creating predictive models, or tracking trends. Decisions are usually based on the sample mean, which is very sensitive to outliers and can dramatically change the value. So, it is crucial to manage outliers to make the correct decision.
Let's consider several simple and fast approaches for working with unusual values.
Problem Formulation
Imagine that you need to conduct an experiment analysis using an average order value as a primary metric. Let's say that our metric usually has a normal distribution. Also, we know that the metric distribution in the test group is different from that in the control. In other words, the mean of the distribution in control is 10, and in the test is 12. The standard deviation in both groups is 3.
However, both samples have outliers that skew the sample means and the sample standard deviation.
import numpy as np
N = 1000
mean_1 = 10
std_1 = 3
mean_2 = 12
std_2 = 3
x1 = np.concatenate((np.random.normal(mean_1, std_1, N), 10 * np.random.random_sample(50) + 20))
x2 = np.concatenate((np.random.normal(mean_2, std_2, N), 4 * np.random.random_sample(50) + 1))
NB that considering metric could have outliers from both sides. If your metric could have outliers only from one side, methods could easily be transformed for that purpose.
Cut Off Tails
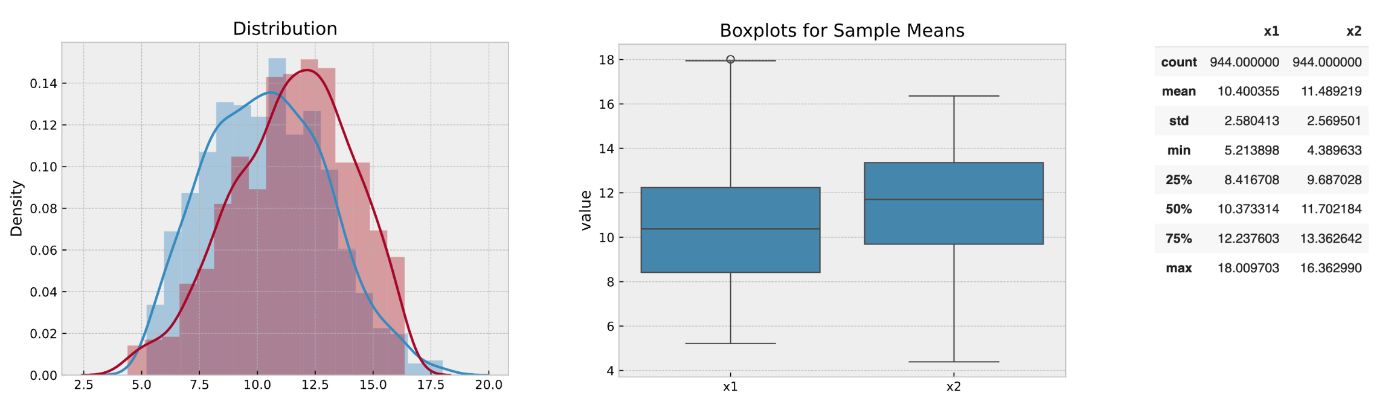
The easiest method is to cut off all observations before the 5% percentile and after the 95% percentile. In this case, we lost 10% of the information as a con. However, the distributions look more formed, and the sample moments are nearer to the distribution moments.
import numpy as np
x1_5pct = np.percentile(x1, 5)
x1_95pct = np.percentile(x1, 95)
x1_cutted = [i for i in x1 if i > x1_5pct and i < x1_95pct]
x2_5pct = np.percentile(x2, 5)
x2_95pct = np.percentile(x2, 95)
x2_cutted = [i for i in x2 if i > x2_5pct and i < x2_95pct]
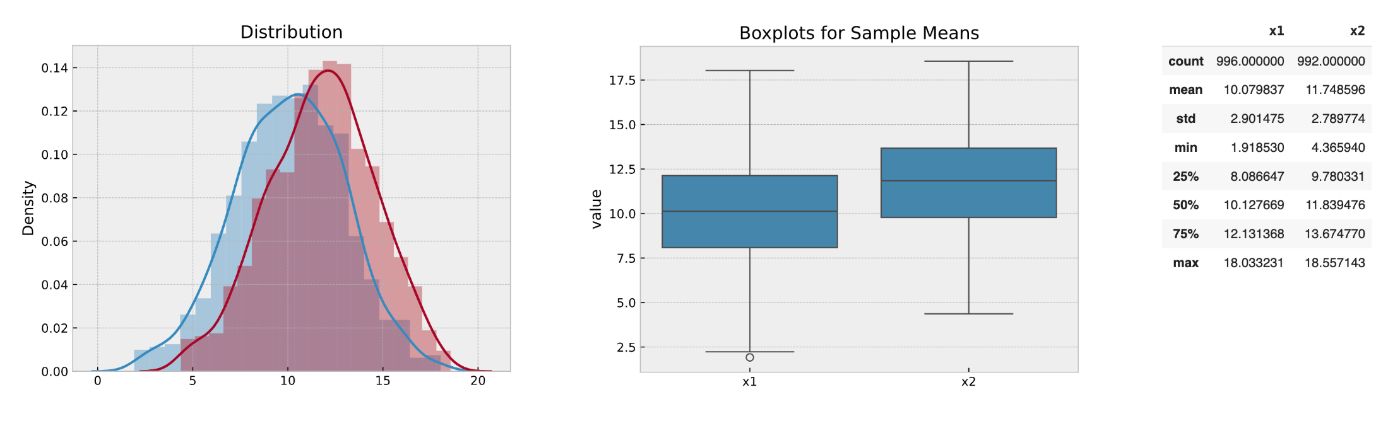
Another way is to exclude observations outside the specific range. The low band equals the 25% percentile minus one-half of the interquartile range, and the high band equals the 75% percentile plus one-half. Here, we will lose only 0.7% of information. The distributions look more formed than the initial. The sample moments are even more equal to the distribution moments.
import numpy as np
low_band_1 = np.percentile(x1, 25) - 1.5 * np.std(x1)
high_band_1 = np.percentile(x1, 75) + 1.5 * np.std(x1)
x1_cutted = [i for i in x1 if i > low_band_1 and i < high_band_1]
low_band_2 = np.percentile(x2, 25) - 1.5 * np.std(x2)
high_band_2 = np.percentile(x2, 75) + 1.5 * np.std(x2)
x2_cutted = [i for i in x2 if i > low_band_2 and i < high_band_2]
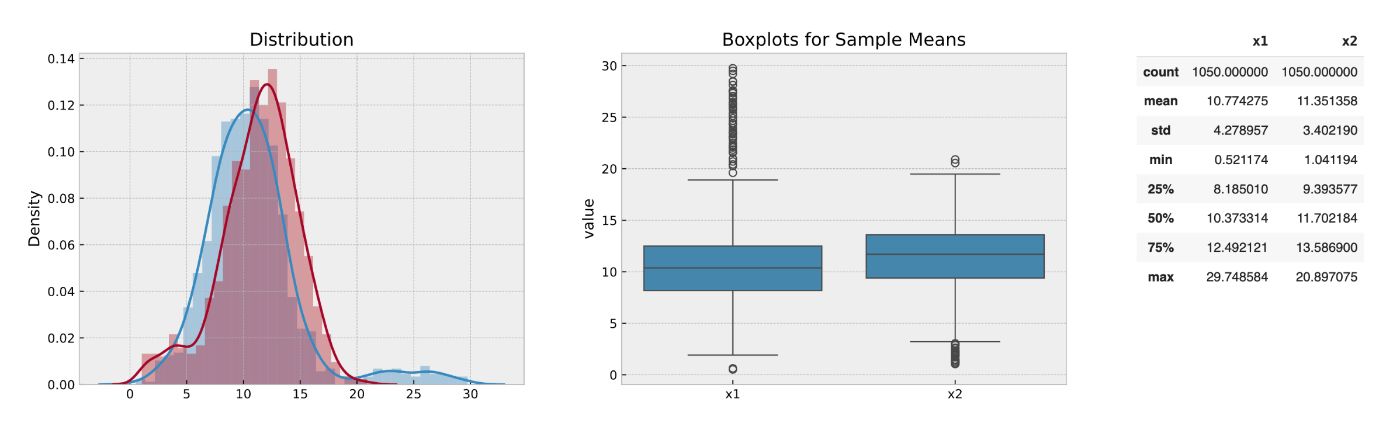
Bootstrap
The second method we considered here is a bootstrap. In this approach, the mean is constructed like a mean of subsamples. In our example, the mean in the control group equals 10.35, and the test group is 11.78. It is still a better result compared to additional data processing.
import pandas as pd
def create_bootstrap_samples(
sample_list: np.array,
sample_size: int,
n_samples: int
):
# create a list for sample means
sample_means = []
# loop n_samples times
for i in range(n_samples):
# create a bootstrap sample of sample_size with replacement
bootstrap_sample = pd.Series(sample_list).sample(n = sample_size, replace = True)
# calculate the bootstrap sample mean
sample_mean = bootstrap_sample.mean()
# add this sample mean to the sample means list
sample_means.append(sample_mean)
return pd.Series(sample_means)
(create_bootstrap_samples(x1, len(x1), 1000).mean(), create_bootstrap_samples(x2, len(x2), 1000).mean())
Conclusion
Outlier detection and processing are significant for making the right decision. Now, at least three fast and straightforward approaches could help you check the data before analysis.
However, it is essential to remember that detected outliers could be unusual values and a feature for the novelty effect. But it is another story :)