This paper is available on arxiv under CC 4.0 license.
Authors:
(1) Falke B. Ø. Carlsen, Department of Computer Science, Aalborg University, Denmark & falkeboc@cs.aau.dk;
(2) Lars Bo P. Frydenskov, Department of Computer Science, Aalborg University, Denmark & larsbopark@gmail.com;
(3) Nicolaj Ø. Jensen, Department of Computer Science, Aalborg University, Denmark & noje@cs.aau.dk;
(4) Jener Rasmussen, jener@jener.dk;
(5) Mathias M. Sørensen, mathiasmehlsoerensen@gmail.com;
(6) Asger G. Weirsøe, asger@weircon.dk;
(7) Mathias C. Jensen, Department of Computer Science, Aalborg University, Denmark & mcje@cs.aau.dk;
(8) Kim G. Larsen, Department of Computer Science, Aalborg University, Denmark & kgl@cs.aau.dk.
Table of Links
3 Model Checking
In order to check if a CGS satisfies an ATL property, CGAAL encodes the problem as an extended dependency graph and finds a fixed-point assignment describing the satisfaction relation.
Extended Dependency Graphs An extended dependency graph (EDG) is a tuple G = ⟨C,E,N⟩ where
C is a finite set of configurations (vertices), E ⊆C×P(C) is a finite set of hyper-edges, and N ⊆C×C is a finite set of negation edges.


3.1 Encoding of ATL in an EDG
We first establish some definitions related to subsets of move vectors induced by a coalition of players.

With this notation in mind, we define the function pmoves. The function pmoves gives the set of all
possible partial moves that follow from the players of the set A ⊆ Σ making a combination of moves in the state q ∈ Q:
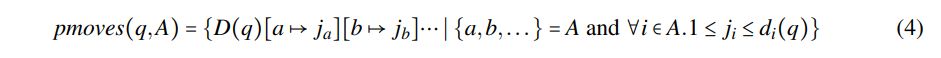
For instance, if D(q) = {1,2}×{1,2} in a 2-player game and A = {1}. Then pmoves(q,A) = {{1}× {1,2},{2}×{1,2}} contains two partial moves. One where player 1 chooses action 1, and another where player 1 chooses action 2. In other words, the pmoves function constructs the partial moves that the set A of players can choose from when working together in the state q. If A chooses V ∈ pmoves(q,A), then V contains all move vectors that result from the remaining players Σ/A also making a choice.
We define a partial transition function ∆ that produces a set of possible successor states given a state q ∈ Q and a partial move V. That is
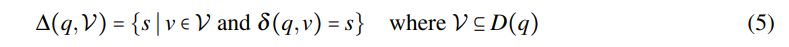
With EDGs, assignments, and partial moves introduced, we can now define how the satisfaction relation ⊧ can be encoded as an EDG.
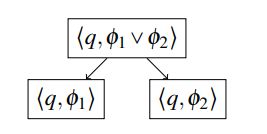
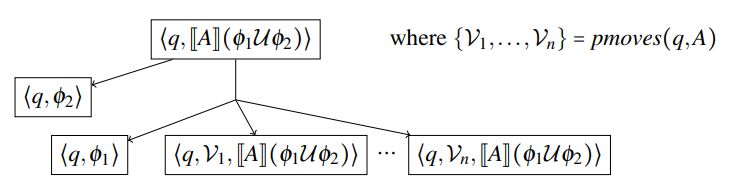
Encoding. Given a CGS S, a state q of S, and an ATL state formula φ we now construct an EDG where every configuration is either a pair of a state and a formula, or a triple of a state, partial move, and a formula. The triples represent partially evaluated states, where some players’ moves are already set. Starting from the initial pair ⟨q,φ⟩, the dependency graph is constructed according to Figures 1 to 6. The figures show which outgoing edges each configuration has and the target configurations of those edges.

The proof of Theorem 3.1 can be found in the extended version of this paper.


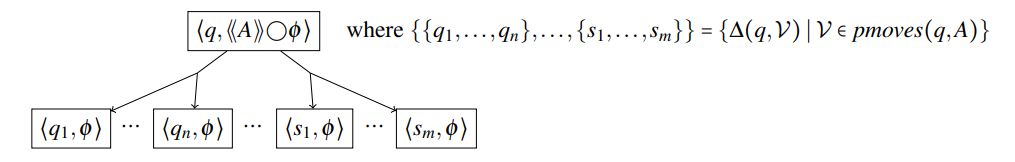

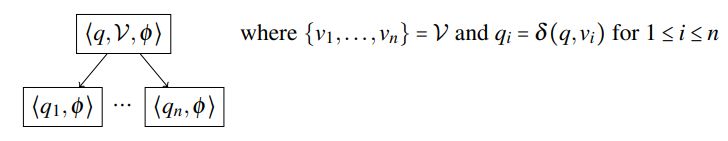
3.2 Search Strategies
The CERTAINZERO algorithm is controlled by a search strategy, which determines in which order the edges are explored and evaluated. Our search strategies for CGAAL include the common breadth-first search (BFS) and depth-first search (DFS) strategies, as well as multiple search strategies based on heuristics. Some of these are discussed in the following subsections. Which strategy is best depends heavily on the shape of the EDG which is determined by the CGS and the ATL formula in question. An evaluation of the strategies can be found in Section 5. The BFS strategy is the default strategy.
Dependency Heuristic Search (DHS) PageRank [15] is an algorithm that was created to estimate the importance of a website based on how many other websites have links to it. The idea has since been used in other areas, such as graph recommendation systems [13] or measuring structural context similarity with SimRank [7]. Our dependency heuristic search (DHS) uses a similar idea by assuming that configurations with many ingoing edges are important. Finding the assignments of these, results in more back-propagation, bringing us closer to termination. In other words, the heuristic focuses on the trunk of the EDG where certain assignments are of high value. Specifically, DHS prioritise edges where the source configuration has a high number of ingoing edges. That is, if e is an edge with source configuration c then:
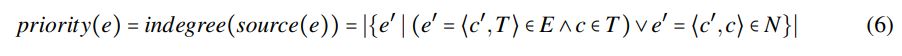
Edges with the same priority are subject to FIFO ordering. However, since we do not know the whole graph in advance, we must continuously update the priority of edges when we explore successors of new configurations. This is only a small overhead with a priority queue data structure.



We also support an alternative search strategy involving linear programming. It is called Linear Representative Search (LRS) and it computes the distance described above for the root configuration only. The closest satisfying state s is then saved and edges are prioritised based on the 1-norm distance between s and the state in their source configuration. In other words, we assume that the state s found for the root represents all satisfied states. As a result this search strategy is cheaper than LPS but risks being inaccurate.
Instability Heuristic Search (IHS) The Petri Net model checker TAPAAL [8] implements the CERTAINZERO algorithm as well. Their configurations consist of a marking (a state) and a property, and their default search strategy uses a heuristic that estimates the distance between the marking of the configuration and a marking that satisfies the formula of the configuration. Our novel instability heuristic is inspired by their heuristic, but we differ by acknowledging that since there are negation edges in the EDG, we may not always be looking for a state that satisfies the formula. That is, if the state already satisfies the associated formula, we estimate the distance to a state that does not instead. This guides the search towards configurations where the assignment is unstable and thus may have a high influence. Algorithms 1 and 2 find the distIHS described above for an edge. The algorithms use an abstract metric BiDist which for state-property pairs finds ⟨tˆ, ˆf⟩ where tˆ is the distance to the property being true and ˆf is the distance to the property being false.


This paper is available on Arxiv under CC 4.0 license.
